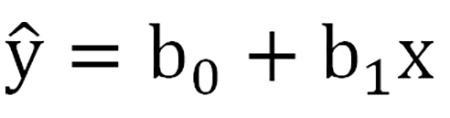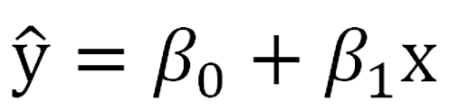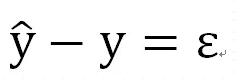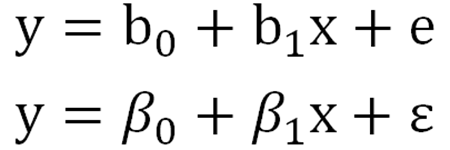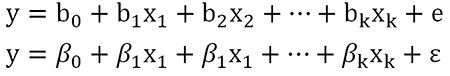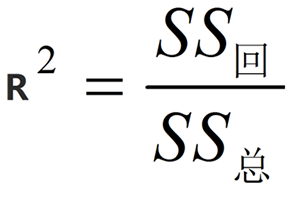构建线性回归必须满足一定的条件,主要包括:
1、2、3在之前一讲已经有所提及,今天介绍第四点的重要性及其诊断方法。线性(Linear)、正态性(Normal)、独立性(independence)、方差齐性(Equal Variance),俗称LINE,是线性回归分析的四大前提条件。LINE条件往往采用残差分析的方法来诊断。若你要掌握线性回归,残差分析必须得学会的基本技巧。线性回归模型构建是否成功,用什么来评价也是重要的内容。SPSS一般来说统计分析时会产生两个指标,R^2和方差分析的P值,本文同时展开介绍。
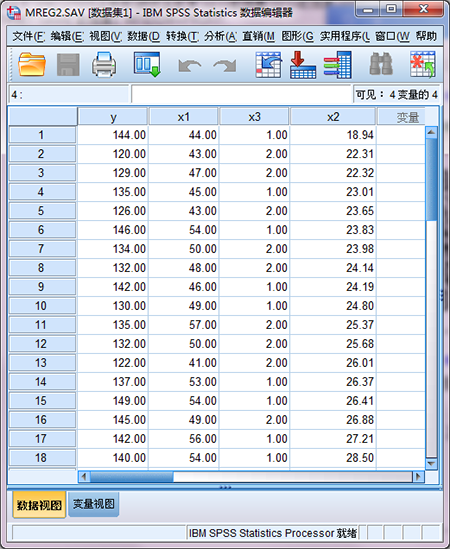
这篇推文将全面介绍多因素线性回归的一些细节处理方法,请不要错过。篇幅较长(约6000字),请耐心阅读。例1:研究究高血压患者血压与性别、年龄、身高、体重等变量的关系,随机测量了32名40岁以上的血压y、年龄X1、体重指数X2、性别X3,试建立多重线性回归方程。数据文件见mreg2.sav。
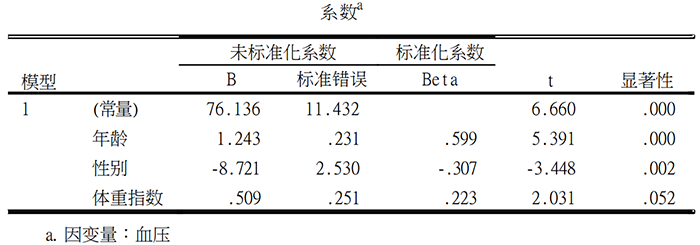
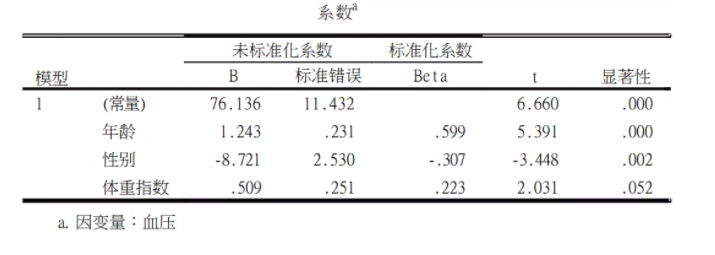
本题应该考虑多因素回归分析方法,结合SPSS得到以下的分析结果:从表格结果来看,年龄对血压的影响的存在着统计学差异(b=1.24,P<0.001);男性相对女性,提高了血压值(b=-8.721,P=0.002),体重指数对血压的影响的没有统计学差异(b=0.509,P=0.052)。线性回归分析,建模型不够,还得包括模型的总体拟合效果评价,模型条件的诊断。若模型诊断和评价结果不理想,上表的结果可能毫无意义。
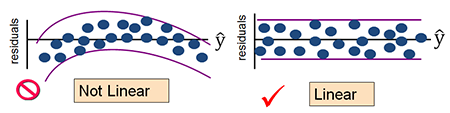
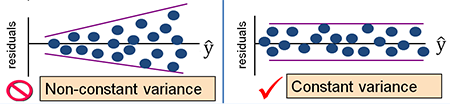
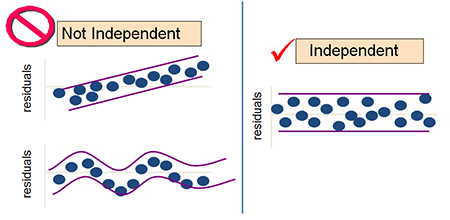
学过医学统计学的往往都知道,不是所有定量数据都可以开展线性回归的,线性回归模型有一些适用条件,简称LINE:线性(L)、独立性(I)、正态性(N)、方差齐性(E)。在这里,我首先严肃纠正一直以来对LINE四个条件的错误理解。很多教材对线性回归LINE语焉不详。给学习统计学带来很多的误导!这种说法本身没错,但没把事情讲清楚,非常容易造成学生的误解。
线性:解释变量X和反应变量Y必须要有线性关系吗?不是!只有当X是定量数据或者等级数据(不设哑变量)时,才要求X与Y有线性的关系。当X是二分类或无需多分类,没有线性条件的要求。独立性:要求Y各观察值相互独立吗? 不是,是要求残差是独立的。正态性:要求Y各观察值正态分布吗? 不是,是要求残差正态分布。方差齐性:要求不同的解释变量X时,反应变量Y方差相等吗?没错,但是对于多因素回归分析,更加合理的理解是在不同Y预测值情况下,残差的方差变化不大。线性回归按自变量数量的多少可以分为:简单线性回归和多重线性回归。简单线性回归只有一个自变量,数学上表达为一元一次函数。其模型可以表示如下:上述公式是基于样本得到的结果,b0和b1均为统计量,若该公式拓展到总体人群,则为其中,关键的指标即为b1和β1,他们称之为回归系数,反映的是x对y的影响力,是当X每改变一个观测单位时所引起y的改变量。值得注意的是,这里x是真实的变量值x,而y带了一顶帽子,并非是y的真实值,而是成为y的预测值或者估计值。实际上,x和y没有严格上一一对应的关系,通过x产生的预测值,是接近于y但不等于y。残差反映了除了x和y之间的线性关系之外的随机因素对y的影响,是不能由x和y之间的线性关系所解释的变异性。可以这么来理解ϵ:我们对y的预测是不可能达到与真实值完全一样的,这个真实值只有上帝知道,因此必然会产生误差,我们就用ϵ来表示这个无法预测的误差。我们通过引入了ϵ可以让模型达到完美状态,也就是理论的回归模型。同样的,多个自变量存在的情况下,多重线性回归模型的表示如下:其中,bk、、βk:回归系数,在多重线性回归中,被称之为偏回归系数,表示每个自变量都对y部分的产生了影响。意义与简单线性回归结果相似,反映的是x对y的影响力,是当x每改变一个观测单位时所引起y的改变量。这里e是样本的预测值与测量值的差别,ϵ是总体中预测值与真实值的差别。戴了帽子的y预测值的变异性是解释变量x们能够预测和解释的。无论e还是ϵ都是无法被预测的变异,是边角料。(1)残差ϵ是一个期望为0的随机变量,即E(ϵ)=0(3)误差项ϵ是一个服从正态分布的随机变量,且相互独立,即ϵ~N(0,σ^2)上述就是为什么线性回归要求残差正态性、方差齐性和独立性的原因。ε一般情况下不知道,因此,我们用e残差来ε代替进行正态性、方差齐性、独立性的分析残差分析,一般可以采用残差的正态性分析和残差图来反映。
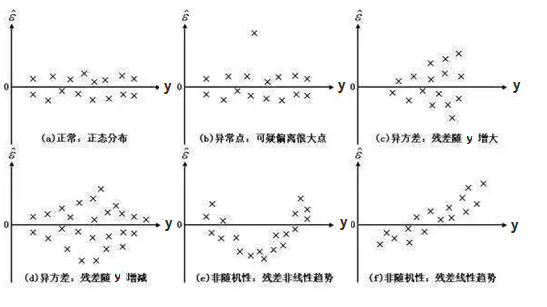
正态性分析可以用绘制残差的直方图或者QQ图来反映,并不复杂。残差图在SPSS软件中是标准化残差与标准化预测值的散点图。各种残差分布下图所示(x轴为标准化预测值,y轴为标准化残差)。根据残差性质,一个好的模型残差分布应是(a)中的分布。(b)中表明数据中可能存在某个异常值,这时需要将异常值删去建立模型,当然要标明此模型不适合该检测值。而(c)表明,残差的方差并不相同,是随着y预测值的增加而增加,所以这就需要对Y进行变换或者其他求解方法来消除这个影响。而(d)也是异方差,随着预测值增加而增减。(d)、(e)中表明Y与X之间存在非线性的关系,需要考虑新的曲线关系,而不再是线性回归。当然也可能Y存在自相关。
线性回归模型SPSS软件给出两个用于评价模型拟合效果的,一个是R平方(R^2),另外一个是方差分析。之前的文章也提过,回归分析就是在探讨结局变量或者因变量变异的来源,究竟是什么造成的。一个回归模型必然有残差,成功的模型必然也有相应的变量来解释y的变异。一般情况下,自变量越多,残差越小,这意味着更多的y的变异被解释掉了。因此多因素回归比单因素更好,更有意义。因此,回归分析时,我们希望残差变异越小越好。残差变异越小,意味着更多的变异被已知的自变量解释了,意味着我们用回归模拟真实世界的效果越好。那么,如何评价回归分析模拟真实现象的效果呢?方法便是计算R^2和开展方差分析
R^2反映自变量能够解释应变量y多大变异性的指标,统计学称之为决定系数。因变量被自变量解释的这一部分变异称之为回归变异,它实际上就是y预测值的变异性,一般用离均差平方和(SS回归)来计算;剩下无法解释的变异就是残差变异(SS残差),变异越大,残差方差越大。SS回+SS残=SS总变异。R^2即SS回归除以SS总变异得到值:决定系数为回归平方和在总平方和中所占百分比,说明模型对真实世界模拟度,0-1,该值越大,模拟度越高,拟合效果更好。R^2用于评价模型好不好,美不美,而方差分析从另一角度评价模型,它探讨模型是否成功构建,有没有意义。它的原理是基于回归均方除以残差均方得到F值,来探讨量是否不是至少有一个解释变量成功地解释了y的变异。如果回答是,那么P值<0.05。若F值很大P值很小,则表明回归均方大而残差均方小,则表明y更多部分被x解释了,模型成功建立。统计分析首先看方差分析结果,判断是否成功建立,在此基础上可看R^2,评价模型是优秀、还是合格。在上一讲教程中,我大致介绍了多因素线性回归SPSS操作,但讲述不全面,没有细致的介绍LINE的分析过程(只说条件是OK的),也没有就R^2、方差分析等进行介绍。本文在上一讲基础上,展开系统的SPSS介绍,来帮助诸位学习多因素回归分析,内容包括x与y的线性关系判断、具体的回归分析方法、残差分析、R^2、方差分析等。对于线性关系的条件,一般要求当x是定量变量或者等级变量时,需绘制散点图探讨与y是否存在着线性趋势的关系;如x为二分类或者无序多分类,无须绘制散点图。这一操作应在回归分析之前完成。
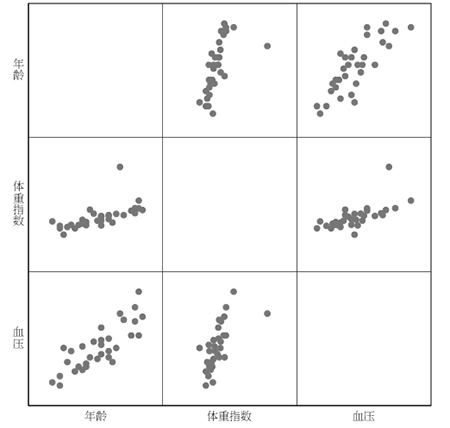
本例开展血压、年龄、和BMI指数的散点图分析。结果发现,体重指数、年龄与血压的线性关系成立。
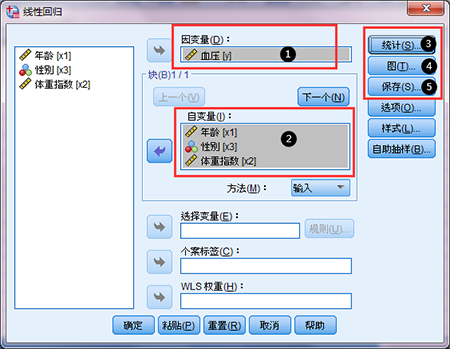
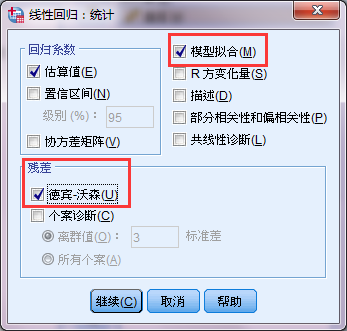
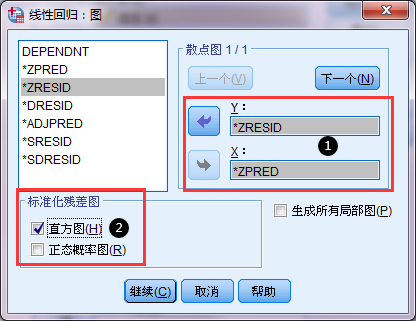
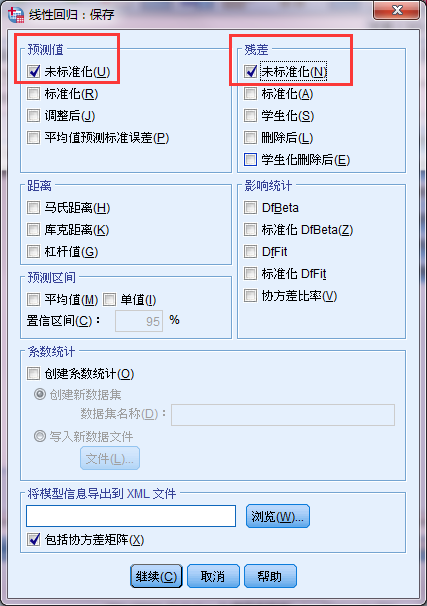
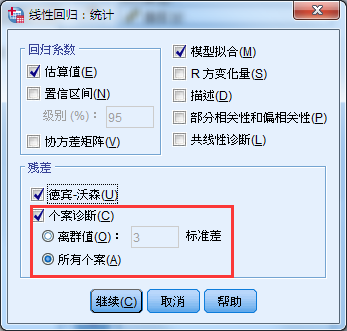
③统计:软件默认勾选模型拟合计算R^2,同时有必要进行残差的独立性分析德宾沃森检验(Durbin-Watson)“图”:可以绘制残差图和残差直方图、QQ图。选择右侧的“图”按钮,将“*ZRESID”选入Y轴,将“*ZPRED”选入X轴(①)(*ZRESID表示标准化残值、*ZPRED表示标准化预测值);②选择直方图(若选择正态概率,将绘制QQ图)
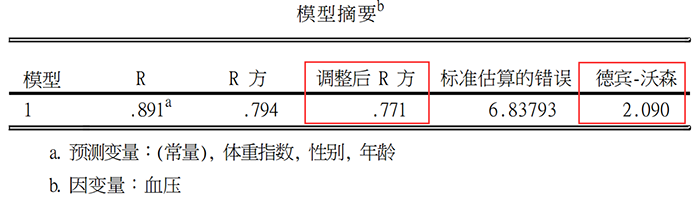
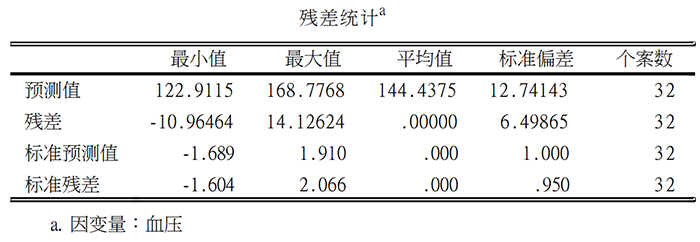
首先呈现的是R^2结果和残差独立性检验(德宾沃森检验)。一般情况下,R^2 看的是“调整R^2”,该值相对不受自变量个数的影响,结果更为可靠。本例调整R^2=0.771,处于较高的水平,也就是说真实世界已经被模拟得“七七八八”了。德宾沃森检验若结果在0-4之间,基本可认为数据独立性符合。本题该值为2.090,独立性符合(该结果同样可以从上文残差分析图可以得到)
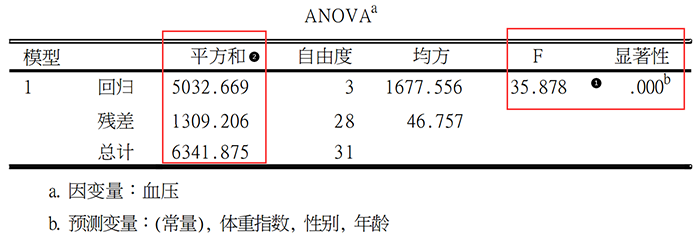
第二个结果为方差分析(ANOVA),主要探讨模型的是否成功建成。本例F=35.878,P<0.001(①),说明至少有一个自变量解释了一部分的因变量的变异,从而使得回归变异变大,残差变异减少,模型成功建立。值得注意的是,本题平方和(②)即变异程度(离均差平方和),回归变异平方和/总的平方和,便是R^2,0.794。因此方差分析和R^2结果同出一源,方差分析侧重于分析模型是否成功,R^2侧重于探讨模型有多成功。第三个结果,回归分析的主要结果:计算回归系数、并对回归系数进行假设检验,探讨影响因素。
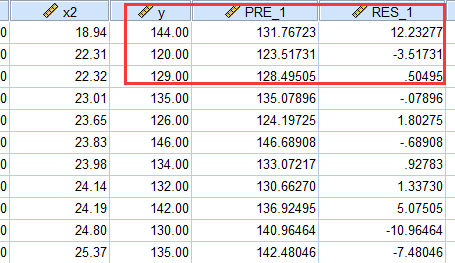
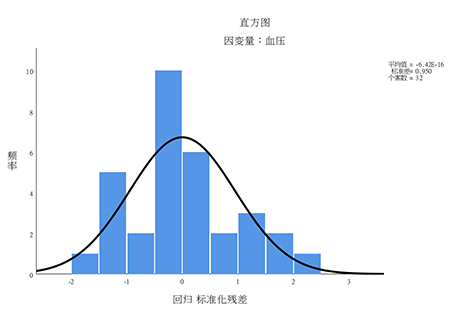
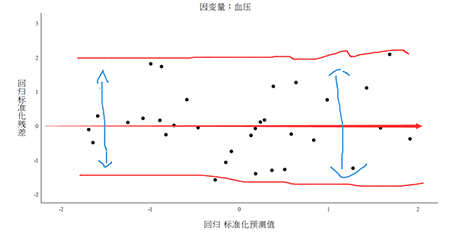
本研究结果显示,年龄对血压的影响的存在着统计学差异(b=1.24,P<0.001);这意味着年龄每增加一个单位(在本研究中一单位等于一岁),血压将上升1.243个单位体重指数对血压的影响的没有统计学差异(b=0.509,P=0.052)。这意味在样本中,体重指数对血压有一定影响,但是回归系数没有通过假设检验的考验,还不能说明总体回归系数不等于0。本结果,难以理解的性别(b=-8.721,P=0.002)。b=-8.721代表什么?到底是男性相对女性,还是女性相对男性?初学者可能比较困惑。b就代表着自变量x每增加一个单位,y改变的量。在本例,性别在数据库赋值分别是1和2,也就是x只改变一次,也就是从1到2,b值改变了-8.721单位。由于数据库赋值1是男性,2是女性,因此结果是女性相对男性,血压更低;男性是高血压危险因素。因此,如果自变量是分类数据,一定要观察数据库是如何赋值的,赋值增加一个单位意味着什么,如此才能看懂回归分析结果。第四个结果,由于本例选择计算残差和预测值,可以通过下表来看预测值和残差结果在数据库中,可以发现增加了PRE_1(预测值)和RES_1(残差) ,两组相加,刚好是y“血压值”。第五个结果,残差直方图。可以看出,本例残差均数接近于0,标准差接近于1,数据呈正态分布(标准正态分布),这意味着线性回归在正态性条件是达到的。第六个结果,残差图。残差图的x、y轴分别是因变量预测值的标准化值和残差的标准化值(一般x轴是预测值的标准化值)。本例从图形来看,标准化残差图分布在0值周围,基本是上下对称分布,分布特征不随预测值的增加而发生改变,意味着数据方差齐性、独立性条件符合。纵观线性回归分析SPSS整个过程,我们要通过散点图解决线性问题,残差分析结局残差的LINE条件,根据R^2和方差分析来评价模型,在此基础,评价各自变量的回归效应。
•线性:如果X和Y的关系是非线性的关系(如曲线关系),则回归系数b值无法值正确反映X和Y 的关系(X是二分类、无序多分类除外)处理方法:将X转为哑变量处理,或者曲线回归,或者对自变量x进行转换(指数转换x^3,或者对数转换log(x)等)。•正态性:如果残差不符合正态性,则可以考虑对y或者x进行数据转换(比如BOX-COX转换),推动残差正态分布;或将y转成2分类或多分类数据采用logistic回归方差不齐:方差不齐可以采用其他方法估计回归系数,常见的如加权最小二乘法估计回归系数•独立性:如果独立性条件不符合,则采用非独立性的数据分析方法,比如线性混合模型、多水平模型、广义估计方程等。很多人、甚至是论文的评审专家很看重R^2,都觉得R^2越大越好,模型越好,对R^2低的模型不屑一看。实际上这些人都是社会学、经济学领域的研究者,对医学研究具体情况不熟悉。医学研究线性回归有几个重要的用途,其中两个分别是预测结局,探讨影响因素。对于目的是预测的线性回归,R^2非常重要,R^2越高,模型预测效果越好,所以经济学领域特别看中R^2。医学研究,偶尔也开展预测,但预测并非医学研究的主要研究目的。实际上,医学研究,由于自变量个数有限,一般情况下R^2都比较小,很难起到预测的效果。如果你觉得R^2应该大才对,实际上你可能误解了一篇文章中线性回归分析 的目的。医学研究开展回归模型,最大的目的是探讨影响因素(或者控制混杂)。在这个目的是,R^2无论大小,都不太影响结果。探讨影响因素,首要探讨的是某一个因素在假设检验中P值到底是否小于0.05。有人说R^2这么小,建模有什么意思?我倒反驳说,就凭医学研究的那几个指标,你就想预测如此复杂的医学现象?痴人说梦!所以,诸位不必纠结R^2是不是过小了!R^2虽好,不必苛求。在实践中,科研工作者鉴别数据异常值是统计分析前首先要完成的工作,否则会导致前功尽弃,得不偿失。比如下图:虚线是代表受异常值影响而偏离的回归线。
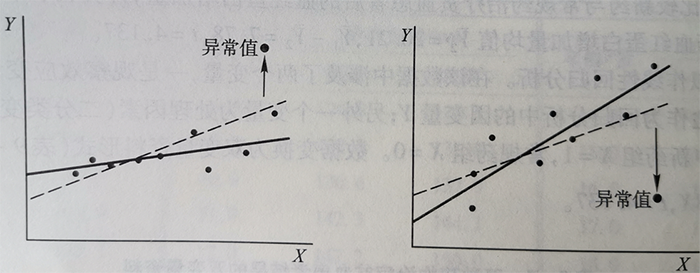
引自:方积乾主编,生物医学研究的统计学方法(第二版)异常值数据的识别可以通过简单、直观、有效的散点图,也可以计算相关统计量(比如残差或者广义平方距离获得)来反映。SPSS软件提供异常值的诊断。可设置一定的离群值标准来诊断存在着异常值的个案(一般是>3个标准差),其残差的直方图也可以看出是否存在着异常的残差值。
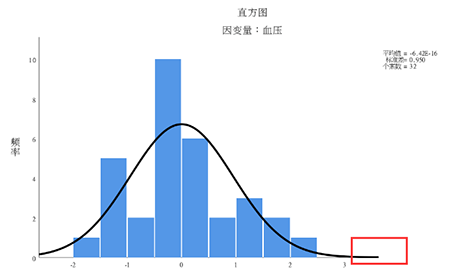
异常残差分布位置,本例残差均小于3个标准差,无特别异常值,红框仅作位置标注
一旦发现可能的异常数据,不易草率地删除,应该仔细审查这些可能异常数据的获得过程。如果是认为实验失误、记录错误或者录入错误等造成的,才考虑删除或者重新测量;若异常值便是个体本身造成,不便删除,否则会扭曲真实结果。
以下文章来源于医学论文与统计分析