识别和控制混杂
(一)控制混杂的必要性和原理
混杂是一种由于暴露因素对某疾病的作用与其他病因对同一疾病的作用在同一个研究里交织在一起所引起的在暴露效应估计上的误差。混杂是一种偏倚,一种在暴露与结局关系上的偏倚,混杂因素必须同时具备一下三个条件(图2):一、是疾病确定的病因或危险因素,即图2里性别必须是肺癌的真正病因或危险因素;二、不是暴露和疾病关系之间的中间因素,如性别不可能是吸烟和肺癌之间的中间因素;三、在目前的研究中与暴露因素有关,即可疑的混杂因素在暴露组和非暴露组存在差异或叫不可比,如吸烟人群中男性占比高于不吸烟人群。结果是,在研究吸烟与肺癌关系的研究中,如果性别是混杂因素,性别将会扭曲吸烟与肺癌的关系,低估或高估吸烟对肺癌危险的作用。
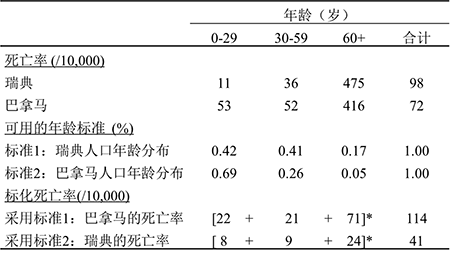
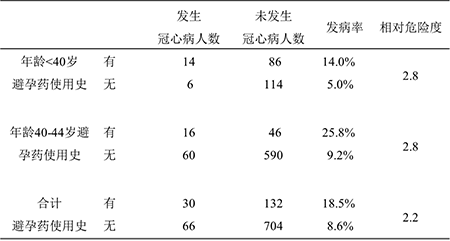
图2 流行病学研究中暴露因素、结局事件和混杂因素 在观察性研究里,混杂是普遍的。因此,观察性研究对混杂的控制是必要的,需控制的因素必须首先符合前两个条件,控制的原理是切断第三个条件,即去除可疑危险因素在暴露组和非暴露组之间的区别或迫使它们可比。对于前两个条件的判断,必须基于现有最好的、来自其他研究的发现或证据,而不是根据目前研究中的结果。如果控制了不符合前两个条件的因素,可能会引起不必要的偏倚。切断第三个条件,指在目前研究中切断第三个条件,从研究设计上有三种方法:限制、匹配和随机分组;在数据分析阶段也有三个方法:直接标化法、分层分析和多元回归。 随机分组(random allocation)使随机对照试验中比较组之间所有可能的已知和未知的混杂因素得到平衡和可比,从而同时切断了所有可能的混杂因素的第三个条件,是所有控制混杂的方法中最简单、最有效的方法,因此随机对照试验无需在数据分析阶段采取混杂控制措施。但是,随机分组只能用于干预性研究,不能用于病因研究。其他控制混杂的方法主要适用于非随机分组的对照试验和观察性研究。 在男性里研究吸烟和肺癌的关系,不会受到性别的混杂影响,因为吸烟组和非吸烟组都是男性,在性别上完全可比,这是限制(restriction)控制混杂的原理。再以性别为例,匹配就是在暴露组和非暴露组纳入同样比例的男性和女性,使两组在性别上可比,从而消除了性别可能引起的混杂,这是匹配(matching)控制混杂的原理。 尽管观察性研究可以使用限制和匹配控制混杂,但是它们在病例对照研究里只能提高统计分析的效率,不能起到控制混杂的作用,反而有可能引入偏倚。在前瞻性研究里,二者都可以有效地控制混杂,但是由于操作上的复杂性,以及由此增加的费用和信息的损失,限制和匹配都不是队列研究(尤其是大型的、需要控制很多混杂因素的研究)用来控制混杂的可行方法。另外,匹配和限制后将不能再分析匹配和限制的因素与结局的关系,尤其在早期探索研究中,二者均会降低研究的效率,也是少用的原因。 因此,绝大多数队列研究和病例对照研究只能在数据分析阶段依靠统计学方法控制混杂。主要方法包括直接标化法、分层分析和回归分析。标化法和分层分析简单、直观、明了,容易理解和解释,是初步认识和控制混杂的最常用的方法。但是它们仅仅适用于一两个因素的控制,同时控制多个混杂因素,只有回归分析是可行、有效的方法。因此多元回归分析是观察性研究识别和控制混杂最重要的方法。 (二)识别和控制混杂的统计分析方法 如前所述,只有真正的病因和危险因素才能成为混杂因素,才需要在具体的研究中进行控制。控制混杂主要依赖分析阶段的措施,而控制混杂之前需识别混杂的存在。识别混杂的关键在于对混杂的第三个条件的认识,即对“混杂因素在目前的研究中与暴露因素有关”的理解。它的确切意思是,在目前的研究中,而不是在任何其他研究中,可疑的混杂因素在暴露组和非暴露组存在差异,存在不可比性。 因此,一个常用的识别混杂方法是,检查真正病因和危险因素在具体研究中暴露组和非暴露组之间的差别。只有组间存在差别的因素,才会引起混杂,才需要进行控制。非真正的病因和危险因素,以及暴露和结局之间的中间因素,即使组间存在差别也不需要控制。这就是各种研究基线比较的目的所在。 但是,在识别混杂是否存在及其大小时,不能根据组间差别的显著性进行判断,组间没有显著性差异不是没有混杂或混杂很小的保证,没有显著性的差异同样可能引起明显的混杂,因为组间差异的显著性还取决于组间差别的大小和样本量的大小,但混杂的大小还取决于混杂因素和疾病之间关系的强弱。比如,每组3人,暴露组男性2人,非暴露组男性1人,组间男性比例的差别没有统计学显著性,显然这不能排除性别可能引起的混杂,而且混杂是明显的。 正确的判断方法是,组间有差异,就有混杂。可见,这种方法仅仅用于识别混杂,而且是间接的、定性的方法,无法确定混杂作用的大小,也无法用来控制混杂。直接标化法、分层分析和回归分析是可以同时用于识别和控制混杂的定量的方法(框2)。 框2 观察性研究分析阶段控制混杂的方法 直接标化法(direct standardization) 分层分析(stratified analysis) 多元回归分析(multivariate regression analysis) (三)直接标化法 混杂的发生是由于混杂因素在比较组间不可比造成的。直接标化法(direct standardization)的原理是在分析阶段研究者“迫使”暴露组和非暴露组拥有同样的混杂因素水平,形成人为的组间可比性,然后在混杂因素分布相同的情况下比较两组的发病情况。现以1962年瑞典和巴拿马死亡率比较为例,说明标化法的原理和方法。 众所周知,北欧的瑞典是一个发达富裕的国家,居民享有很高的平均寿命,而中美洲的巴拿马是一个欠发达国家,生活水平、医疗标准和平均寿命均低于瑞典。然而,表3资料却显示,1962年瑞典人口的年总死亡率为万分之98,高于巴拿马的万分之72,两国的粗死亡率之比(即相对危险度)为1.36,说明生活在(或暴露于)瑞典是一个死亡的危险因素。这显然是一个错误的结论。 表3 1962年瑞典和巴拿马粗死亡率和标化死亡率的比较 注:方括弧中的数字是该组实际死亡率与标准年龄构成之积,如22≈53×0.42,相当于该国家死亡人数在不同年龄组的相对比例,不是年龄组的死亡率。资料来源:Rothman KJ. Modern epidemiology. 1st ed. Chapter 5 Standardizationof rates. Boston: Little, Brown and Company, 1986.41-50 仔细检查两国人口年龄组死亡率发现,瑞典0岁-29岁和30岁-59岁年龄组的死亡率均低于巴拿马,只有60岁以上年龄组的死亡率高于巴拿马,但是瑞典60岁以上人群在总人口中的比例是巴拿马的3.4倍。这说明瑞典总死亡率高于巴拿马的假象很可能是因为年龄在两国分布不同(即瑞典平均年龄高于巴拿马)而造成的混杂偏倚。而且瑞典60岁以上年龄组的死亡率高于巴拿马,还是由于瑞典这个年龄组的平均年龄高于巴拿马,年龄越高越容易死亡。 一种公平的比较方法是假设两国人口的年龄分布(即每个年龄组人数的百分比)是一致的,并“迫使”这个“新的人口”分别“经历”两国的实际年龄组死亡率,然后估计和比较两个国家的标化年龄后的总死亡率,这样就可以消除年龄造成的混杂。这就是直接标化法。 在上述的直接标化法里,标化的标准是年龄分布。在本例中,有两个方便的标准可以使用:瑞典人口的年龄构成(表3中的标准1)和巴拿马人口的年龄构成(表3中的标准2)。标化只需要一个标准。假如我们采用瑞典人口的年龄分布作为标准计算标化死亡率,则瑞典的总死亡率维持不变(万分之98),而巴拿马按照瑞典人口构成的标化总死亡率为万分之114,标化率的相对危险度RR=98/114=0.86。若用巴拿马人口的年龄构成作为标准,则巴拿马的总死亡率不变(万分之72),而瑞典的标化总死亡率为万分之41,相对危险度为0.57。使用不同的人口标准,都显示瑞典的总死亡率低于巴拿马,这是消除了年龄构成不同后的比较,是符合常识也是符合事实的结论。 本例分析中粗率的相对危险度(RR=1.36)为含有年龄混杂的效应估计,标化率的相对危险度(RR=0.86)是消除了混杂作用后的准确的效应估计,若二者相同,则说明年龄没有在比较两国总死亡率中引起混杂;若二者不同,则说明年龄引入了混杂,二者差别的大小反映了混杂作用的大小。在混杂存在与否的问题上,标化法是可靠的,但是在估计混杂大小的问题上,使用不同的标准经常会得出不同的结论,反映了标化法的问题。 另外,标化法还有间接标化法(indirect standardization)。在比较两个组时,间接标化法和直接标化法在本质上(即按照混杂因素的分布标化)没有任何区别,但是在比较三组或更多组别时,间接标化法相当于使用“游动”标准进行标化,这样可疑危险因素的分布在各组势必是不同的,因此是不合理的,不能消除混杂的作用,一般情况下应避免使用。 (四)分层分析 分层分析(stratified analysis)就是根据混杂因素的特征,将研究对象划分成几个小的“独立的研究”,一个独立的研究就是一个层,然后分别估计每个独立研究中暴露对结局事件的作用。例如,在研究吸烟和肺癌的前瞻性研究中,已知性别是肺癌的危险因素,可能引起混杂,因此可以按照性别将研究对象划分成两个独立的层,男性一个层,女性另一个层。 在每一个层内,吸烟和肺癌的关系不再受性别的影响,在层内控制了性别可能引起的混杂,因此每个层内的效应估计是准确的、无(性别)混杂的。如果每层效应的大小是一致的,可以进而用加权平均的方法计算出各层加权平均的总效应,这个总效应消除了性别的混杂,因此是无(性别)混杂的准确的估计。最后,将准确的总效应与无分层时估计的粗的总效应进行比较,如二者无区别,说明粗效应没有性别的混杂,是准确的;如二者有区别(即任何实际的差别,包括无统计学显著意义的差别),说明粗效应有性别的混杂,应弃之,最后使用加权平均的总效应作为无偏倚的效应估计。 在分层分析中,中心问题是各层别之间效应值的一致性。首先是对一致性的判断,其次是不一致时对各层异质结果的处理。由于随机误差的存在,层别效应估计值完全相等的机会几乎是零,不一致才是常态。其次,组间效应的大小可能存在真实的差别,比如吸烟在男性中引起的肺癌的危险的确高于女性。那么,层间的不一致性则由机会和真实的层间差异两种因素造成。 因此,分层分析的一个重要任务不是判断层间效应估计之间是否存在差异,而是这个差异的原因是什么。由于随机误差永远存在,而真实的层间差异可能存在,也可能不存在,不一致性的解释只有两种可能:一、仅仅由于随机误差造成,二、由随机误差和真实差异两种因素造成。处理层间差异首先是区别以上这两种情况。通常使用的方法就是一致性检验(homogeneity test),又叫异质性检验(heterogeneity test)。如果异质性检验显示差异有统计学显著性(p≤0.05),说明是第二种情况,提示可能存在交互作用(见下)。反之,说明是第一种情况,说明层间差异可能完全是由于随机误差造成的,各层的真实效应是一样的,完全可以用一个总效应概括各层的效应,这个总效应就是前面提到的加权平均总效应,或叫调整总效应。 加权就是根据不同层别效应估计值的精确度给以不同的权重,一般来讲权重与样本量成正比,因此加权可以看成是给予样本量大的层或亚组更多的信任。最简单的最原始的方法就是依据样本量的大小进行加权。常用的加权平均法包括DerSimonian-Laird法,Mantel-Haenszel法,以及Peto法。DerSimonian-Laird法是最通用的方法,适合于所有效应测量指标,其权重就是效应估计的标准误平方的倒数。Mantel-Haenszel法只可用于二分变量的数据,Peto法只可用于比值比。鉴于计算机软件的普及性,这些估计很容易通过计算机获得,这里不做赘述。框3总结了分层分析的步骤。 ①确定暴露、结局和混杂(或效应修饰)变量 ②计算暴露对结局作用的粗效应值(如粗RR) ③按照混杂因素把研究对象分成两层或多层(即多组) ④计算各层暴露对结局作用的层效应值(如层RR) ⑤用异质性检验判断组间效应值的一致性 ⑥如果异质性检验无显著性,计算加权平均的调整效应值 ⑦比较粗效应值和调整效应值,若二者有别,说明存在混杂 ⑧用调整效应值做为无(该因素)混杂偏倚的总效应值 ⑨如果异质性检验有显著性,提示可能存在交互作用(或曰效应修饰作用) 现用表4中一个虚拟的前瞻性研究的数据,说明如何使用分层分析来识别和控制混杂作用。该研究的暴露是口服避孕药,结局指标是冠心病,混杂因素是年龄。该分析按照年龄将研究对象分为两组,两组口服避孕药和冠心病的RR都是2.8,粗RR为2.2。由于组间RR没有区别,调整RR还是2.8。粗RR和调整RR存在差别,说明存在年龄的混杂。无混杂的效应估计是2.8。 表4 分层分析:口服避孕药、年龄和冠心病关系的前瞻性研究(虚拟数据) (五)多元回归分析 多元回归分析(multivariate analyses)是利用多元回归模型进行流行病学数据分析。多元回归分析的优点是很容易估计主效应、分析交互作用和剂量反应关系,还可同时控制多个混杂因素,统计效率高。流行病学数据分析使用最多的回归模型之一是Logistic模型回归。利用计算机软件(如SPSS)分析时,可在回归方程的左边放入做为因变量的结局事件,在回归方程右边放入做为自变量的各种危险因素,包括暴露因素、混杂因素和可能的效应修饰因素。每个自变量的回归系数就是该变量对结局作用大小的指标,具体说就是该因素和结局关系比值比的对数值,其反对数就是该因素的比值比。同时,这个比值比也是控制了方程内所有其他危险因素的无偏倚的估计。回归分析同时还提供了每个因素比值比的标准误、p值及其95%可信区间。 如何在回归分析里识别混杂的存在呢?在此问题上,一个常见的错误是利用潜在混杂因素效应的显著性检验来判断混杂存在与否,如果检验是显著的,则该因素是混杂因素。其实,该检验的本质是对该因素与结局关系比值比的显著性检验,即在目前研究中检验混杂的第一个条件“该因素是疾病确定的病因或危险因素”,因为是基于目前的研究,有关结论是不可靠的。即使该检验是可靠的,它也不能验证混杂的第三个条件“该因素在目前的研究中与暴露因素有关”,因此不能作为判断混杂存在的方法。逐步回归自动筛选纳入或去除变量的根据是统计学检验的p值,因此也不是筛选混杂因子可靠的方法。 混杂是一种偏倚,造成主效应(principal effect)(即暴露因素对结局事件的效应)估计的误差。回归方程同时可以控制方程内所有因素的混杂作用,因此给出的主效应是一个无(这些因素)混杂的效应估计。由此,判断某因素是否可能引起混杂的一种方法是,将该因素从包含所有潜在混杂因素的回归方程中剔除,然后重新估计主效应的大小,如果主效应的大小发生了改变,说明该因素是混杂因子,应在最后分析时纳入回归方程,控制其混杂作用;否则,该因素不是混杂因素,无需进行控制。当然,也可以采取逐步加入混杂因素的方法进行判断。但这样做比较麻烦,同时也不能排除使用不同的变量剔除或加入顺序时结论可能不同的可能性。因此,一般的做法是将所有的潜在混杂因素同时都纳入回归方程,并依据此方程估计主效应的大小,并不对每个可疑混杂因素对主效应的作用进行评估。这样做法的好处是,简单易操作,且调整的总效应是准确的,但引入的非混杂因素会降低回归分析的统计学效率。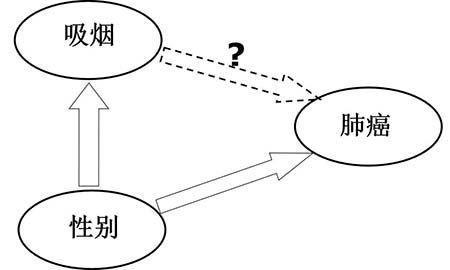
原文出处:唐金陵. 第二十章: 流行病学研究数据统计分析概述. 见: 李立明 主编. 《流行病学》. 第一卷. 第三版. 北京: 人民卫生出版社: 2015: 369-397.
作者:唐金陵,广州市妇女儿童医疗中心临床研究总监、香港中文大学流行病学荣休教授














