进行系统综述时,有时对一个定义、方法或程序可能存在两种(或多种)似乎同样合理的选择,研究者不能确定哪个更好。这时可以对原定义、方法和/或程序做适当的“改动”,这个变动可能会改变个别研究的合格性和/或个别研究的数据的赋值,依据新的研究数目和数据,重新进行meta分析,并与原分析结果比较,评估原meta分析的结果的稳定性和可靠性,这样的分析就叫做敏感性分析(sensitivity analysis)。
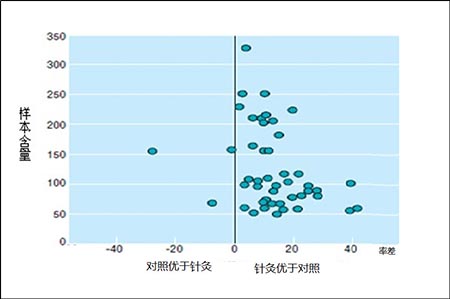
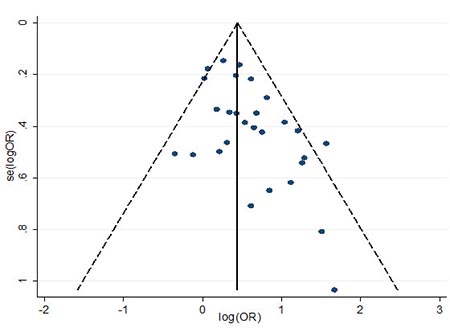
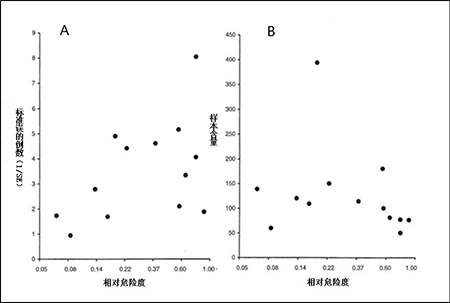
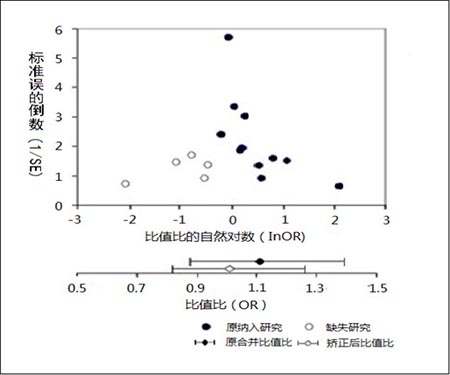
如果敏感性分析结果与原分析结果相比没有本质的区别, 那么敏感性分析就会加强原分析结果的可信度。如果敏感性分析结果与原分析结果不同, 则需谨慎解释原分析的结果。敏感性分析中可改变或修正的内容包括以下几个方面: 1. 研究类型和研究质量,如排除仅有的个别观察性研究或低质量的研究; 2. 研究对象、干预措施及结果的定义和测量,如排除仅有的不同治疗剂量的研究; 3. 纳入和排除标准,如排除少数某种族的研究; 4. 数据提取方法和缺失数据的估计方法,如换一种方法提取某个数据点; 5. 统计模型,如使用不同的权重方法。 重要的是,对研究中的定义、方法和/或程序的修改必须有足够的理由,主要理由是对它们的不确定性,而且改变定义、方法和/或程序的结果只能涉及极个别研究,不能涉及很多研究,否则即说明原始研究定义方法和程序本身可能存在问题。另外,根据研究结果进行的敏感性分析属于事后分析,有很大的主观性,应尽可能避免,下结论应十分慎重。例如,发现meta分析里一项研究的结果十分特殊,然后主观地找个理由将其剔除,再进行分析。这样的分析就属于与结果相关的事后分析。 举例说明,在Karagiannis等在2012年发表的评价降糖药物二肽基肽酶Ⅳ抑制剂疗效的系统综述中,作者合并了所有7个二肽基肽酶Ⅳ抑制剂对比二甲双胍的研究发现,二甲双胍在降低糖化血红蛋白方面优于二肽基肽酶Ⅳ抑制剂,组间均数差为0.2,95%可信区间为(0.08, 0.32)。敏感性分析中,作者排除了两个低质量的研究后重新分析,发现对结果没有明显影响,均数差为0.26,95%可信区间为(0.14, 0.38)。该敏感性分析加强了原分析结果的可信性。 发表偏倚的检测和矫正 一、漏斗图的构建和解释 系统综述中的偏倚可分为选择偏倚、信息偏倚和混杂偏倚。选择偏倚是系统综述中最重要的偏倚形式,发表偏倚是系统综述特有的常见的选择偏倚,主要是由于小型阴性研究发表的机会小于大型和/或阳性研究。在研究实施阶段,与研究者和有关机构联系,搜集未发表的研究,是减少发表偏倚的常用方法,但是效果往往不好。解决发表偏倚的有效策略是实行研究注册,研究注册在临床试验方面已经十分普遍。但是,注册数据的利用尚处在初级阶段,且不能解决过去没有发表的研究的问题,而且对观察性研究关注较少。 在数据分析阶段,目前普遍使用的检测和矫正发表偏倚的方法是基于漏斗图发展起来的一套方法。以研究结果作为横坐标,以样本量作为纵坐标,将一项meta分析里的研究绘成一个散点图。如果这些研究来自同一个总体,代表的是同一个真实值,这些研究结果的散点会形成一个对称的倒置漏斗形状的图形,系统综述里把这类散点图叫做漏斗图。漏斗图是用来测量发表偏倚的重要工具。 在漏斗图里,小样本研究坐落在下部,大样本研究坐落在上部,且围绕图形横轴的中心点呈对称分布。由于小样本研究效应值的变异程度较大,精确度较低,因而其结果分布比较分散,与中心值的平均距离较远。相反,大样本效应值的变异程度较小,精确度较高,因而其结果分布比较集中,与中心值的平均距离较近。研究结果与中心值的距离随样本量的增加而减小,散点图呈倒置漏斗状。 当发表偏倚存在时,即部分或全部小型阴性研究没有发表,漏斗图底部显示治疗无效的一侧会变得稀疏或完全缺失,使整个图形失去对称性,不对称性越明显,发表偏倚的可能性就越大,meta分析高估真实结果的程度就会越大。 图3展示了42个评价针灸治疗卒中效果的随机对照试验的结果,是一个以样本量为纵坐标和干预效果(率差)为横坐标构成的漏斗图。这些研究的结果基本分布在无效线的右半部分,绝大多数研究都是阳性结果,显示针灸可以降低卒中的发生率,图形呈明显的不对称分布,显示可能存在严重的发表偏倚。 图3 评价针灸预防卒中效果的42个随机对照试验的漏斗图 (引自:Tang JL, et al. BMJ 1999; 319: 160-2) 值得注意的是,研究发现,样本量不是漏斗图纵坐标的最优选择,建议最好使用效应指标对应的标准误或其倒数作为纵坐标。在使用率比和比值比等相对效应指标时,横坐标应取效应量的对数值,纵坐标应取相应的标准误或其倒数值。出于对漏斗图对称性判断的需要,一般来讲绘制漏斗图需要足够的研究数目,有人建议至少需要5个独立研究,研究数目过少,由机遇造成的漏斗图不对称性的可能性会大增。 二、漏斗图的对称性检验 漏斗图是检测发表偏倚的重要工具,其不对称性提示发表偏倚可能存在。用肉眼观察判断漏斗图的对称与否是不可靠的,存在很大的主观性。同一个图,一个人可能认为是对称的,另一个则可能会认为是非对称的,反之亦然。对漏斗图非对称性的判断,应该依赖客观、定量的分析方法,如Begg秩相关性检验和Egger回归分析,都是检验漏斗图对称性的定量的统计学方法。 Begg秩相关性检验的统计量是秩相关系数,检验的是效应值与其方差(或标准误)的秩的相关关系。秩就是按照效应值和方差大小进行排序所得到的位次。如果漏斗图是对称的,那么效应值与其方差的秩应呈线性相关关系。当秩相关系数有显著统计学意义时,说明漏斗图是不对称的,可能存在发表偏倚。一般来讲,该方法的检验效能较低,结果没有显著统计学意义时,并不能排除发表偏倚存在的可能。 检验对称性使用更多的是Egger回归分析。该回归分析是以效应值的标准正态离差为因变量以其精确度为自变量进行的加权线性回归分析,权重为标准误平方的倒数,检验的统计量是回归方程的常数(即截距)。以比值比为例,比值比的标准正态离差等于比值比的对数值与其标准误的商,精确度等于标准误的倒数。如果漏斗图是对称的,那么回归方程的截距应等于零,有显著统计学意义的非零的截距说明图形是不对称的,即小型的研究显示的效应与大型研究不同。当截距为正数时,说明小型研究的效应小于大型研究;当截距为负数时,说明小型研究的效应大于大型研究,提示部分小型阴性研究可能没有发表,因此可用作发表偏倚可能存在的证据。另外,Egger也建议使用效应值和其标准误的加权回归系数作为分析的统计量,详情不再赘述。 仍以表3中尼古丁替代疗法系统综述的数据为例,利用Stata软件制作的以比值比的对数值为横轴,以其标准误为纵轴的漏斗图见图4。Egger回归分析的结果显示,漏斗图不对称(t=3.08,P=0.005),并提示有发表偏倚的存在。 图4 Stata软件生成的尼古丁替代疗法戒烟效果meta分析的漏斗图(注:该漏斗图横轴为log(OR)) Egger法的敏感性高于Begg法。但是,当研究少于20个时, 两者的敏感度均较低。此外,还有很多其它类似的方法,在哪一种更好的问题上,尚没有一致的意见。另外,有时未发表的研究可能多是显示效应不存在的研究,即比值比等于或接近1的研究,在漏斗图中将呈现底部中心值附近的空洞现象。这种选择性发表在病因学研究里更为普遍,不会对总效应估计产生偏倚,只是降低效应值的精确度。 三、非对称性漏斗图的解释 负的Egger回归常数显示的本质是,小型研究的效应大于大型研究,提示发表偏倚的存在。但是,发表偏倚不是这类漏斗图的唯一原因,不对称的漏斗图可由以下几种解释。 (一)发表偏倚 负的Egger回归常数说明小型研究的效应大于大型研究。如前所述,小型阴性研究不被发表的机会大于小型阳性研究和大型研究,致使小型研究的平均效应大于大型研究,因此负的Egger回归常数揭示的可能是发表偏倚。 (二)真实的异质性 某些情况下小型研究效应大于大型研究的异质性可能真实存在。例如,小型研究经常是在理想的优良干预环境里进行的,而大型研究则是在现实的一般干预环境中进行的,这时小型研究的效应一般都会大于大型研究,并不是发表偏倚的结果。小型研究也可能使用了较大的治疗剂量,或是更高的治疗频率,或是在高危人群中进行的,因此实际效应可能大于大型研究。另外,小型研究也可能存在更多的方法学问题,或可能有造假,或分析方法不当,夸大了真实效应。 (三)文献检索的问题 小型阴性研究的缺如未必是选择性发表引起的。也可能是由于小型阴性研究多不在英文杂志发表,或是被引用机会较少,或是重复发表机会较小,因此不易被发现和收集。但是,漏检了小型阴性研究对合并结果的影响与发表偏倚无异。 (四)效应指标的选择 不对称的漏斗图也可能是横轴和纵轴选择的问题。以二分类变量数据为例,漏斗图横坐标可选用的效应指标包括比值比、率比、率差等,同时又有多种纵轴指标可以选择,如标准误、标准误的倒数和样本量,所产生的漏斗图的形状(尤其是对称性)可能不一样,因此关于发表偏倚的结论可能不同。 唐金陵教授1994年的一项研究显示,在43个显示可能存在发表偏倚的meta分析中,如果使用不同的纵轴和/或横轴,37(86%)个漏斗图的不对称性会发生转变,提示发表偏倚并不存在。举例说明,图5展示了基于同一组临床试验的两个漏斗图,横坐标都是率比,纵坐标分别为标准误的倒数(图5-A)和样本量(图5-B)。 图5 采用不同纵轴指标时漏斗图不对称性的比较 (引自:Tang JL, et al. J Clin Epidemiol 2000; 53: 477-84) 结果显示,基于样本量的漏斗图是对称的,而基于标准误的图形是不对称的。除非我们可以肯定哪种构图方法是正确的,否则我们将无法确定哪种漏斗图的结论是正确的,因此就无法利用漏斗图客观地判断发表偏倚的存在。这是使用漏斗图测量发表偏倚的最大缺陷。 (五)机遇 另外,由于统计学检验一类错误的存在,有时漏斗图的不对称性可能仅仅是由于机遇引起的,并不存在发表偏倚。 四、发表偏倚的矫正 漏斗图可以用来识别发表偏倚。如果认为发表偏倚可能存在,可借助剪补法(trim and fill method)对合并的结果进行调整,以分析发表偏倚对合并结果的影响。 剪补法是一种迭代算法,其基本思想是先去除漏斗图不对称部分的小样本阳性研究,以得到对称的漏斗图,并计算合并的总体值,然后将去除的这些小型阳性研究以及相应“缺失”的阴性研究填入前次估计的总体值的两侧,重新计算效应值,如此反复,一直到漏斗图以总体值估计为中心左右对称分布为止,最后估计的总体值就是矫正了发表偏倚的估计,如果矫正的效应值与未矫正的效应值相比,没有明显的差别,则说明发表偏倚不存在,或即使存在偏倚也很小。 从这个意义上讲,剪补法还可以用来识别发表偏倚,尤其是当meta分析纳入的研究数目小于20时,即Begg秩相关检验和Egger回归分析识别发表偏倚的敏感性较差时。填补缺失的研究后进行效应量的估计是一个大胆的假设,合理与否尚无定论。值得注意的是,如果非对称性不是发表偏倚引起的,利用剪补法进行矫正是没有意义的。 举例说明。一项研究神经节苷脂降低急性缺血性脑卒中患者死亡率的系统综述纳入了11篇随机对照试验,从图6可以看出,11个研究(黑色实心圆点)构成的漏斗图是不对称的,可能存在发表偏倚。采用剪补法进行矫正,在漏斗图的左下方对称性地填补了10个代表缺失的阴性研究(空心圆圈),新的漏斗图呈对称分布。没有矫正的比值比为1.11,95%可信区间为(0.88, 1.39),矫正的后的比值比为1.01,95%可信区间为(0.82, 1.26),二者点估计存在差异,没有矫正的结果高估了实际效果。但是,由于二者结果没有实质性的区别,所以可以认为原始结果是可信的。 图6 利用剪补法对11项研究结果矫正前后的漏斗图及合并效应值 (引自:Rothstein HR, et al. Publication Bias in Meta-Analysis: Prevention, Assessment Adjustments. Chichester: John Wiley & Sons, 2006, pp. 127-144.) 五、漏斗图的正确使用 从一方面讲,不对称的漏斗图有多种可能的解释,发表偏倚只是其中一种;从另一方面讲,由于研究数目小,有关检验灵敏度低。因此,发现不对称的漏斗图,不能证明发表偏倚真实存在;对称的漏斗图也不能证明发表偏倚一定不存在,可能因为研究数目太少,或者更换横轴和/或纵轴指标,对称性可能会消失。一般来讲,当研究数目小于10个时,漏斗图的对称性检验基本没有什么意义。另外,当研究结果都远离无效线时,即使发表偏倚存在,对合并效应的影响只是量的差别,不会改变其方向。 以研究治疗效果的系统综述为例,正确的做法是,发现不对称的漏斗图时,只能暂且认为它是发表偏倚引起的,并进行矫正,如果矫正前后的结果差异不大且都没有显著统计学意义,就可以做出治疗无效的结论。如果矫正前后的结果存在差异且都有显著统计学意义,这时应假定发表偏倚存在,定性的结论是一致的,但定量结果最好以比较保守的矫正后的结果为参考。 如果矫正前后的结果存在差异,且矫正前的结果显示有显著统计学意义,校正后的结果没有显著性或是方向相反,这时应尽可能排除漏斗图非对称性的其它原因,才能认为发表偏倚可能存在。例如,如果通过亚组分析或回归分析,发现小型研究质量较低,这时可以放弃小型研究,只依赖真实可靠的大型研究做出结论。又如,如果小型研究和大型研究结果的差异可由一些重要的临床因素解释,如小型研究干预环境优于大型研究,或者小型研究治疗强度高于大型研究,这时应分别报告大型研究和小型研究的结果,以便使用者根据实际情况区别对待,不能简单地按照发表偏倚处理。 原文出处:唐金陵, 毛琛. 第三十一章: 系统综述中的统计分析. 见: 李立明 主编. 流行病学. 第一卷. 第三版. 北京: 人民卫生出版社, 2015. 作者: 唐金陵,广州市妇女儿童医疗中心临床研究总监、香港中文大学荣休教授 毛琛,南方医科大学公共卫生学院流行病学系主任,教授