本文转载自:张天嵩,董圣杰,杨智荣,武珊珊,田金徽,孙凤*. 网络Meta分析研究进展系列(十三):生存数据的网络Meta分析[J]. 中国循证心血管医学杂志. 2021;13(6):649-652
在生物医学领域,有很多研究感兴趣的结局是到某个事件发生的时间,发生的事件可以是不利结果(如死亡、肿瘤复发等)、有益结果(如怀孕、出院等)、中性结果(如停止母乳时间)",这类数据称为至事件时间数据(time-to-event data),传统上称为生存数据或生存资料 (survival data)、随访资料(follow-up data)。
对该类数据行的统计分析称为生存分析,主要考察每个研究对象出现某一结局所经历的时间,广泛应用于恶性肿瘤、慢性疾病等随访研究中事件分析,比如疾病的发生、复发、转移、伤口的愈合、某种症状的消失等。
生存数据具有独特的特点:①至事件发生的时间趋向于偏态分布,则采用正态似然不适合;②在随访期内并非每例患者都出现待观察的事件,即有截尾观测。
在生存数据中,结局事件和发生时间同等重要,主要的分析方法为风险或生存函数。针对生存数据进行经典的Meta分析和网络Meta分析(network meta-analysis, NMA),与连续型数据和二分类数据相比更加棘手,既不能简单地将时间作为连续型数据处理,也不能把事件简单地作为二分类数据处理。
生存数据NMA,一般可分为一步法和两步法两种分析策略,一步法适用个体参与者数据(individual participant data,IPD);两步法适用于IPD和聚合数据(aggregate data,AD),目前多使用两步法。
本文主要梳理基于两步法生存数据NMA的相关方法和模型,以期为研究人员了解和开展相关工作提供参考。
1、生存数据类型
1.1 个体参与者数据
理想情况下,系统评价员能够获得纳人NMA每个原始研究的IPD,收集到原始研究的起点事件和终点事件及相关人数、生存时间、影响因素(协变量)等。IPD既直接用于一步法NMA建模;也可采用适合的模型计算出单个研究的尺度参数和位置参数,然后进行NMA效应量合并。
1.2 聚合数据
如果不能获得原始研究的IPD,则需要依赖于研究水平的聚合数据如相应的概括统计量(summary statistics)。一般情况下,报告的生存数据效应指标多为生存率、生存期、生存风险比/危险比(Hazard ratio,HR)等。
其中,生存率指标主要有总生存率(overall survival,OS)和无进展生存率(progression-free survival,PFS)等,有时也会报告在某个时间点患者存活比例(时点生存率)等;生存期指标主要有平均生存期、中位生存期、无病存活期、无“事”存活期(event free survival,EFS)等。
但在实践中,HR是用来比较不同组别至事件时间干预效应最常用、最合适的指标,但遗憾的是有不少研究并未直接报告HR,但可以通过其他统计量转换或从Kaplan-Meier (K-M)曲线中提取来获得,计算HR及其方差的主要方法如表1所示。
表1. HR及其方差的计算方法

2、效应量计算
在系统评价和Meta分析中,生存数据最合适的效应量是HR,如果不能获得IPD,则需要小心采用相应方法从研究中水平来获得HR及相应统计量,本文重点讨论从概括统计量转换或从K-M曲线中估算HR。
2.1 时序检验
Tierney等[1]提供了基于研究的报告信息如何从单个研究中计算HR及相应统计量,并给出大量公式、详细解释、实用例子和基于 Excel开发的计算工具,非常有参考意义。
例如,假设能从时序检验(log-rank test)获得实验组相对于治疗组的lnHR可通过(O-E)/V来估计,标准误为1/√V。式中O为每个研究中实验组事件发生数,E为实验组期望发生事件数,(O-E)为log-rank统计量,V为log-rank统计量的方差。
一项新辅助化疗治疗口咽癌研究的时序检验结果如表2所示,则根据公式很容易的获得HR的对数及相应方差或标准误,分别为:

2.2 Cox比例风险回归模型
在纳人Meta分析的随机对照或队列研究中,常用Cox比例风险回归模型(Cox proportional hazards regression models,简称Cox回归模型)来计算HR,一般会直接给出校正后的HR值及其95%可信区间。
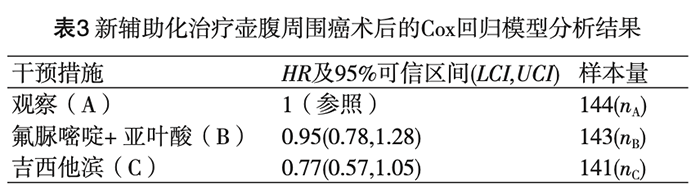
有时,多臂研究中存在两个及以上的干预措施,但只报告相对于同一参照(如安慰剂)的相对干预效应,如一项新辅助化疗治疗壶腹周围癌术后患者的临床研究,将性别、吸烟状态、干预措施等作为调节因素纳入Cox回归模型进行分析,选取干预措施相应结果如表3所示,共分为三个治疗组,分别为观察组、氟脲嘧啶(fluorouracil)联合亚叶酸(folinic acid)组、吉西他滨(gemcitabine)组。
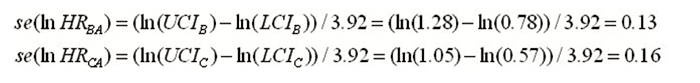
其次,根据Woods法获得C vs. B风险比的对数尺度及相应近似标准误:
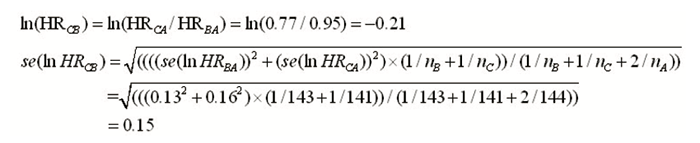
2.3 Kaplan-Meier曲线
K-M曲线法是一种用于评估风险函数的非参数方法,不需要对生存时间的分布进行特殊指定,并图示化结果显示数据的风险函数估计。如果原始研究采用K-M曲线报告了OS、PFS等生存结局,则可从中获得随时间变化的生存比例等数据。
如Guyot等建立了一种算法,可从已发表的K-M曲线中重建“伪(pseudo)”IPD,从而获得相应的HR等效应量,可用于进行经典的Meta分析或NMA。国内已有学者[2]介绍了采用图形数据提取软件(如Engauge Digitizer软件)处理K-M曲线、提取数据,并计算HR及其方差的具体操作过程,均可供参考,本文不再赘述。
2.4 二分类数据或计数数据转换
有的研究可能报告了时点生存率,但未报告获HR等其他数据,如果没有截尾值,可通过相对危险度(RR)或者比值比(OR)替代计算HR,但RR或者OR并未考虑时间因素,与HR相比丢失了一些重要的信息,故这种处理方法不作为常规选择。
新近Watkins提出了一种合并二分类数据与HR的简单方法,与Woods法异曲同工,其中也提供了二分类数据(计数或比例)转换为HR的方法:为简单起见,假设每个两臂研究中的臂为k(k=1,2),每个臂的总人数为nk,时间为t*上观察到事件发生人数为rk(t*),或比例pk(t*)=rk(t*)/nk(t*),则HR的对数尺度及相应标准误分别为:
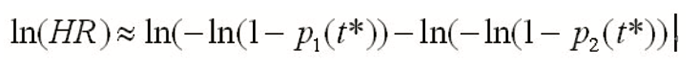
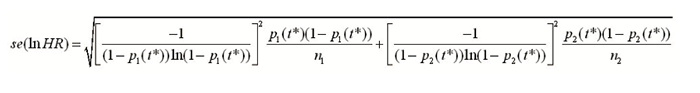
3、生存数据NMA模型
3.1 图论法
3.1.1 基本模型
由Rücker等基于电网理论提出。假设在NMA中有n个不同干预措施(点),存在m个比较(线),显然,如果纳入的均为两臂研究,则m为纳入分析研究的个数,假设干预措施(点1,...,n)和研究(边1,...,m)按固定顺序任意编号。
令向量y=(y1,L,ym)T和w=(w1,...L,wm)T分别表示观测效应量及其抽样方差倒数,并定义对角线m ✕ m矩阵W=diag(w),含有研究(边)在其对角线线上的权重wi,令Wy为经方差倒加权观测效应(wiyi)i的点乘向量。
为了给定比较,首先要定义网络结构,Rücker引入几个非常重要的概念,一是边点发生矩阵(edge-vertex incidence),是m ✕ n设计矩阵,行表示研究(边),在同一行中,某列用“1”表示干预措施(点)所在研究(边)的起点,“-1”表示终点;
二是拉普拉斯矩阵(Laplacian matrix),是n ✕ n矩阵,定义为L=BTWB;三是拉普拉斯矩阵的摩尔-彭若斯广义逆(Moore-Penrosepseudoinverse)矩阵L+=(L-)-1+J/n,其中,J为含1的n ✕ n矩阵。通过这些矩阵,可以计算直接比较和间接比较的方差,进而估计Q统计量、成对比较的效应量等。
3.1.2 软件实现
如果能够获得每个研究中配对比较干预措施的HR及其方差或标准误,该模型可通过R软件的netmeta包拟合来实现。netmeta包是基于频率框下NMA的R软件扩展包,由Rücker等编写,目前版本为1.3-0,于2021-1-18发布,需要在3.5.0及以上版本的R软件运行[3]。
该包的数据输人格式、计算编程极其简单易行,感兴趣的读者可阅读其自带帮助文件或相关文献介绍。
3.2 参数化生存曲线法
3.2.1 基本模型
参数化生存曲线(parametricsurvival curves)法由Ouwens等与Jansen提出,是用参数化生存曲线的参数替代HR建模。假设ln(hjkt)表示第j个研究第k个干预措施在时间点的风险率(Hazard rate);向量
为研究特定效应,用来表示基线干预(baseline treatment)b的尺度参数v。和形状参数θ;向量
表示第j个研究中干预措施威布尔生存曲线在尺度参数和形状参数θ上的差异,可通过合并由参照干预 (reference treatment)表达的效应估计来刻画;∑表示协方差矩阵,用来表示异质性;σ1和σ2分别表示在尺度参数v和形状参数θ上的异质性,ρ表示两参数的相关性,则两臂研究的NMA随机效应模型为:

该模型虽然以威布尔分布为例,但从原理上而言,也适用于其它参数化生存分布,如龚帕兹分布(Gompertz distribution)、对数逻辑斯谛分布(Log-logistic distribution)、对数正态分布(log-normal distribution)等。
3.2.2 软件实现
Ouwens等提出的模型在贝叶斯分析框架下由WinBUGS/OpenBUGS、JAGS、R等软件来拟合。实际上,文献中[4]给出了模型的WinBUCS程序代码、数据输入格式、实例数据分析等,可供参考;研究者们也可以根据分析目的、数据类型、软件功能和自己对软件的掌握程度等方面来综合考虑选择其他合适的软件。
3.3 分段多项式模型
3.3.1 基本模型
分段多项式(Fractional polynomials,FP)是一族灵活参数模型,用于描述变量间的相关性,模型假定随时间变化干预效应不呈线性变化。Jansen等提出将FP模型应于NMA中,如将第s个研究中第j个干预措施M阶次FP结构的测量平均值定义为:

其中us表示研究平均值,δj表示干预措施j相对于参照干预的研究和时间特定效应,协方差矩阵∑表示干预效应参数δmsj的研究间异质性。
令t0=ln(t);模型中感兴趣的协变量(时间)幂次p从S={-2,-1,-0.5,0,0.5,1,2,3}中选取;阶次为m=1,L,在医学应用中,一阶和二阶转换最常见,故M选1和2即可。
3.3.2 软件实现
Jansen等提出的模型可以在贝叶斯分析框架下,由WinBUGS/OpenBUGS、JAGS、R等软件来拟合。文献中[5]给出了模型的WinBUCS程序代码、数据输入格式、实例数据分析等,可供参考。
4、结语
当前,尚无明确的指南或推荐意见用于指导生存数据进行NMA。理想情况下,直接利用IPD建模进行统计分析。如果不能获得IPD,则针对 AD有两种主要建模方法,一是拟合HR数据,但需要注意的是,合并分别由时序检验和Cox回归得到的HR统计量时要小心,因为后者一般是得到了校正;一是拟合基于K-M曲线重建的伪IPD。
建议在实践中要报告这两种分析方法的结果:如NMA网络中含有足够的K-M曲线数据,推荐基于分段多项式模型展示结果;如NMA网络中没有足够的K-M曲线数据,则推荐展示基于HR的NMA分析结果。
本文转载自:
中国循证心血管医学杂志. 2021;13(6):649-652.














