一、主成分分析简介
在对于一件事物的研究过程中,为了准确的反映事物间的关系,往往需要收集多维指标,以保证尽可能全面地收集信息。然而多维指标往往会提高分析人员的分析难度,并且相似变量也造成了信息重叠,不利于准确提炼数据关系的本质。
主成分分析法(PCA)就是一种常见的降维算法,它能够降低数据维度,减少高维数据分析难度。主成分分析法能够在实现降维的同时,能够尽量的保证信息损失。因此在很多分析工作中,可以通过提炼主成分的方式,仅依靠少数几个线性组合代替原先的数据集,既提高了数据分析效率,又避免了数据信息的过多损失。
二、R包介绍
FactoMineR包是主要用于多元统计分析的R包,它能轻松实现主成分分析、因子分析、聚类分析等多元统计分析方法,并提供对分析结果做可视化的分析工具。factoextra包也是多元统计分析包的主要组件,它主要用于提取多元统计分析结果,并进行可视化探索。本文将基于FactoMineR包和factoextra包进行主成分分析。
FactoMineR包的主要函数:
PCA:用于主成分分析的方法
HCPC:层次聚类分析法
MCA:多重对应分析
MFA:多因素分析
FAMD: 混合数据因子分析
CA : 对应分析
factoextra包的主要函数:
fviz_pca:可视化PCA分析
fviz_mca:可视化多重对应分析
fviz_hmfa_var:可视化多因素分析
eclust:可视化聚类分析结果
三、数据简介
使用Datasets包里的mtcars数据集作为主成分分析的测试数据。mtcars数据集记录了32种不同品牌的轿车的的11个属性,分别为:
mpg: 数值型,车辆油耗,单位是每加仑英里数
cyl: 数值型,气缸数
disp: 数值型,发动机排量
hp: 数值型,马力数
drat: 数值型,后桥速比
wt: 数值型,车身重量,单位为千磅
qsec: 数值型,四分之一英里加速时间
vs: 数值型,V/S
am: 数值型,0=自动挡,1=手动挡
gear: 数值型,前进档位数
carb: 数值型,化油器数量
四、主成分分析可视化
本文采用FactoMineR包的PCA方法进行主成分分析,并以factoextra包进行分析及可视化。
library(FactoMineR)
library(factoextra)
library(datasets)
res.pca <- PCA(mtcars, graph = FALSE,scale.unit=T)对于主成分分析,首先需要判断选择多少个主成分合适,一般可以选择特征值大于1的主成分。可以通过factoextra包的get_eigenvalue函数来输出特征值,具体见下图。
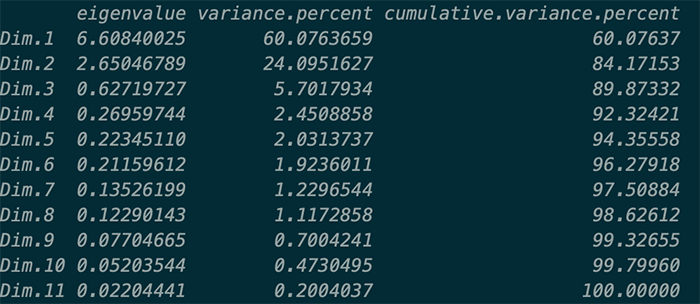
eigenvalue为特征值,variance.percent为主成分的方差贡献率,cumulative.variance.percent为累积防擦好贡献率。除了通过特征值设定阈值外,还可以通过特征值的累积贡献率来选择主成分数量。
1.碎石图
通过各主成分的方差贡献率,可以绘制如下这张碎石头图:
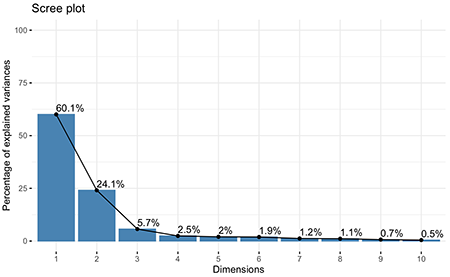
从碎石图上看,前三个主成分的累积贡献率接近90%,因此可以考虑选择前三个主成分输出。
除了特征值外,还可以通过get_pca_var函数来提取主成分分析结果中的其它变量。
var <- get_pca_var(res.pca)
2.变量相关图
通过fviz_pca_var函数,可以展示变量与主成分间的相关关系。我们以cos2这个指标为例,cos2反映了各个主成分中各个变量的代表性,一个变量的所有主成分cos2值加起来等于1。对于主成分而言,某个变量的cos2越接近1,则说明变量对该主成分的代表性越高;cos2越接近0,则说明变量对该主成分的代表性越差。我们以第一、第二两类主成分为例:
fviz_pca_var(res.pca, col.var = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07")
)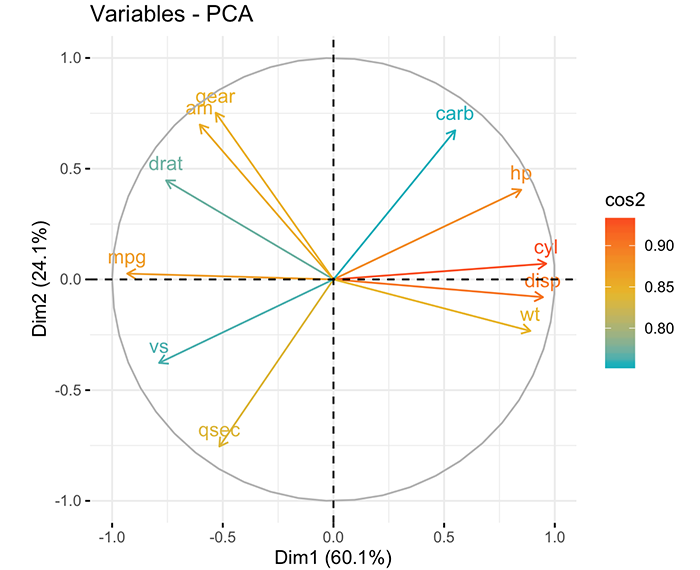
上面这张图为变量相关图,反映了变量与主成分之间的相关关系,图上的变量越接近圆周,则表示该变量对主成分的代表性越强;越接近圆心,则表示该变量对主成分的代表性越差。各变量到各个维度的距离则表现各变量对该主成分的代表性,即cos2。从图上看,mpg、cyl、disp、wt对第一主成分具有较高的代表性,但是对于第二主成分则不具有显著的代表性。
3.变量贡献图
fviz_contrib()则展示了各变量对主成分的贡献图,以第一、第二、主成分为例:
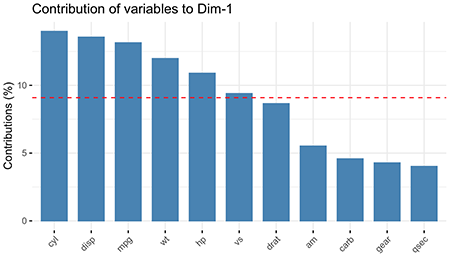
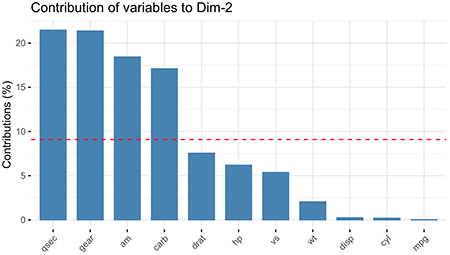
红线表示各变量的平均贡献率。
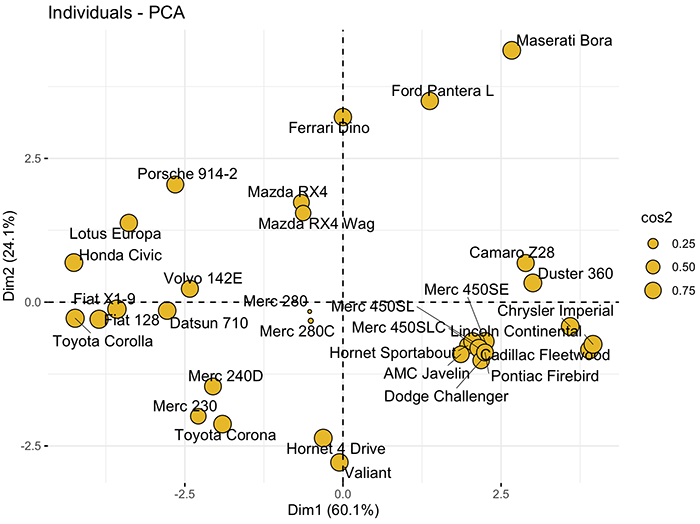
4.主成分样本散点图
对于给定的样本点,可以对样本点的主成分得分与主成分进行相关关系展示,以此来区分个样本点的区别与相似。
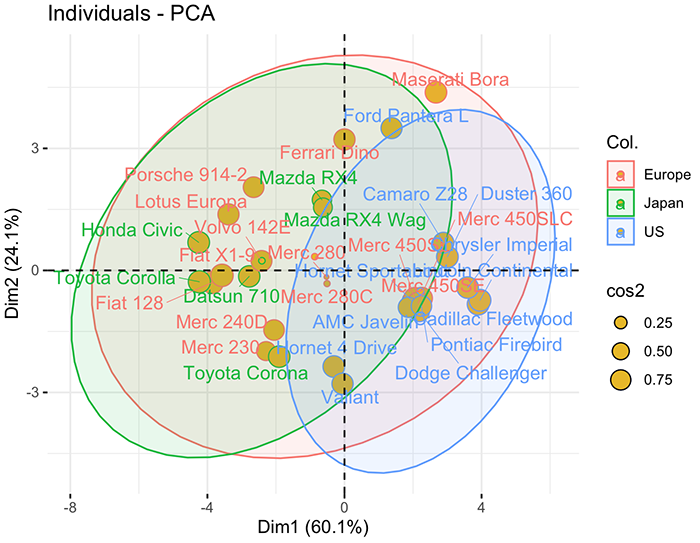
如果按照汽车品牌的国家分类的话,还可以在图中对样本点进行分组:
文章来源于R友舍














